最大似然估计
目录
最大似然法
- 极大似然估计方法 (Maximum Likelihood Estimate,MLE) 也称为最大概似估计或最大似然估计,是求估计的另一种方法,我们用已知的样本数据分布去推测具体的分布情况。
- 通俗来说,最大似然估计的目的就是就是利用已知的样本结果信息,反推最具有可能 (最大概率) 导致这些样本结果出现的模型参数值!
- 换句话说,极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。假设我们要统计全国人口的身高,首先假设这个身高服从服从正态分布,但是该分布的均值与方差未知。我们没有人力与物力去统计全国每个人的身高,但是可以通过采样,获取部分人的身高,然后通过最大似然估计来获取上述假设中的正态分布的均值与方差。
使用极大似然估计方法的两个条件:
- 我们假定数据服从某种已知的特定数据分布型。
- 我们已经得到了一定的数据集。
一般步骤
这部分来自:https://www.cnblogs.com/BlairGrowing/p/14877125.html 求最大似然值的一般步骤: 1. 写出似然函数; 2. 对似然函数取对数,并整理; 3. 求导数 ; 4. 解似然方程


来自:https://blog.csdn.net/zouxy09/article/details/8537620
要求 θ,只需要使 θ 的似然函数 L (θ) 极大化,然后极大值对应的 θ 就是我们的估计。这里就回到了求最值的问题了。怎么求一个函数的最值?当然是求导,然后让导数为 0,那么解这个方程得到的 θ 就是了(当然,前提是函数 L (θ) 连续可微)。那如果 θ 是包含多个参数的向量那怎么处理啊?当然是求 L (θ) 对所有参数的偏导数,也就是梯度了,那么 n 个未知的参数,就有 n 个方程,方程组的解就是似然函数的极值点了,当然就得到这 n 个参数了。
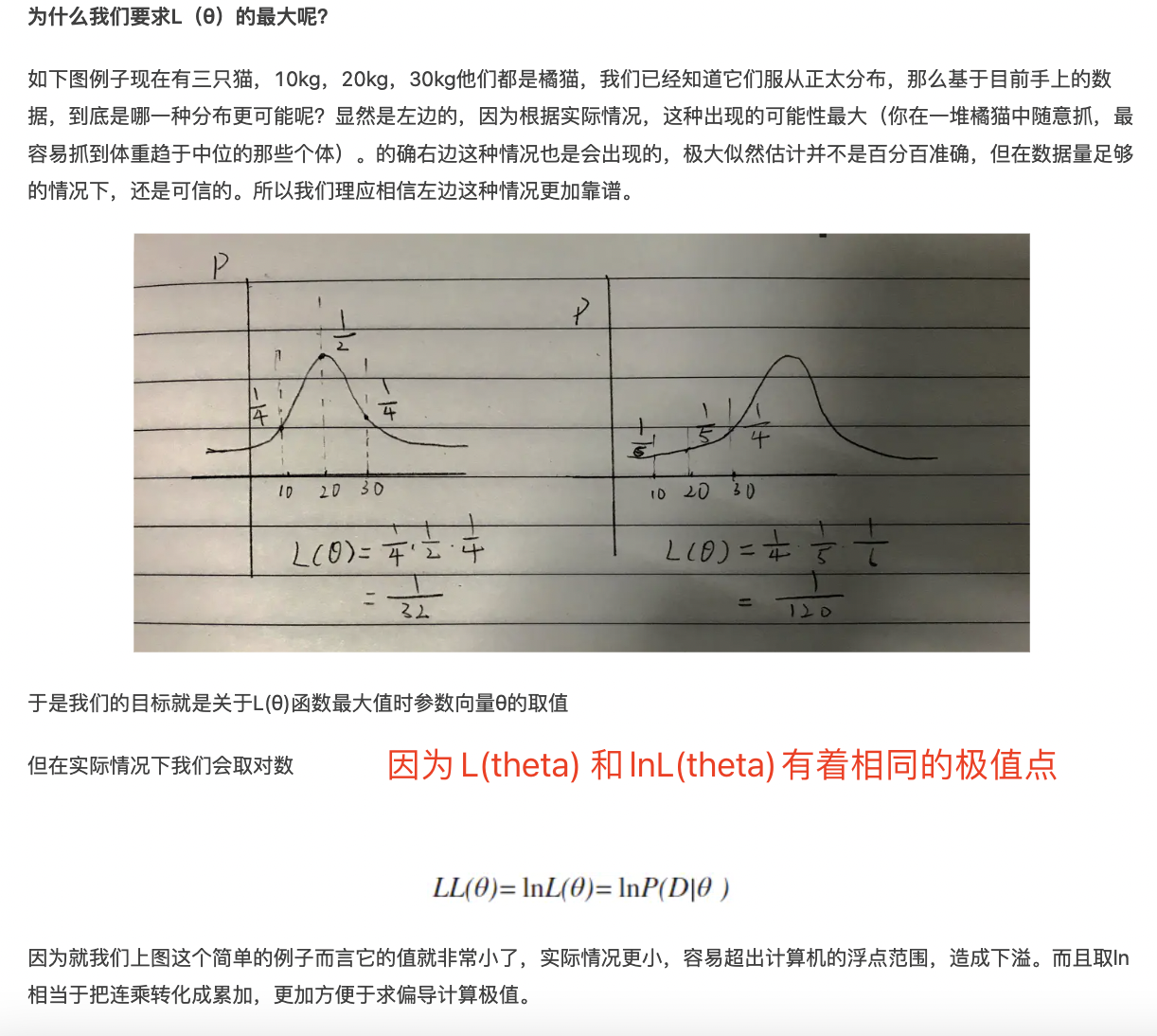
举例
橘猫分布情况
根据现实经验和科学道理,我们可以确切得到两个条件。 1. 动物的体重分布是符合正态分布的。(也可以说我们假定它服从正态分布) 2. 我们抓住了学校里所有的橘猫,得到了 100 只橘猫的体重。
那么如何用这 100 只橘猫的数据集 D 去推测橘猫具体的体重分布呢?
我们将这 100 只橘猫体重设为数据集 D:D={x_1, x_2, ... , x_100}

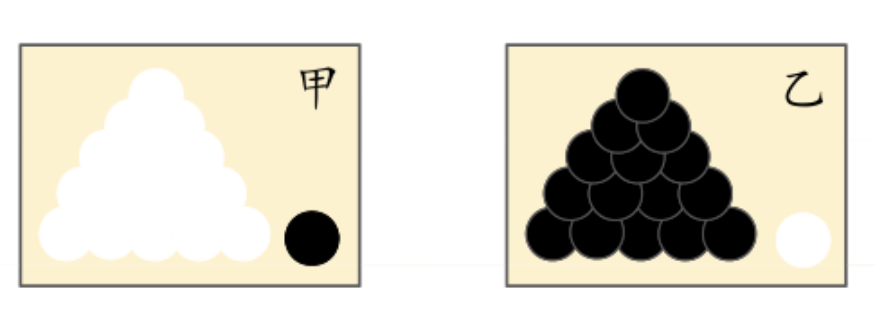
离散型例子
有两外形相同的箱子,各装 100 个球,一箱 99 个白球 1 个红球,一箱 1 个白球 99 个红球,现从两箱中任取一箱,并从箱中任取一球,问:所取的球来自哪一箱?答:第一箱。

感谢参考文章中大佬们写的文章,很清晰,我这里只是搬过来辅助自己理解,虽然已经看晕了
